En las simulaciones que utilizan el método de los elementos finitos, la malla tiene una importancia crucial. Este artículo describe las características esenciales de un estudio de convergencia de malla para determinar el refinamiento de malla necesario para obtener resultados suficientemente precisos.

General

Las simulaciones realizadas mediante el método de los elementos finitos se basan en lo que se conoce como discretización. En este caso, un problema con solución desconocida se descompone en subproblemas para los que puede determinarse una solución aproximada. En el caso que nos ocupa, se trata de una descomposición geométrica en componentes (elementos) finitos (finitos) cuyo comportamiento físico puede describirse aproximadamente mediante funciones de aproximación. De ahí la importancia de realizar un estudio de convergencia de la malla. La malla de EF suele refinarse iterativamente, partiendo de una malla gruesa. El objetivo de este estudio es seleccionar una malla que proporcione resultados suficientemente precisos. Se busca un término medio. Por un lado, la malla debe ser lo suficientemente fina como para que un refinamiento adicional no suponga un aumento relevante de la precisión, pero, por otro, debe ser lo más basta posible para conservar recursos (tiempo de cálculo/espacio de memoria). Alcanzar el límite de convergencia, es decir, menos de un 1% de cambio en los resultados entre los pasos, indica una solución estable. En general, es más probable alcanzar la convergencia para los desplazamientos que para los resultados de orden superior, como las tensiones y deformaciones. Es importante seleccionar un punto especial para la monitorización, ya que el cambio de la malla también puede conducir a un cambio de las coordenadas de los nudos de la malla de EF. En RFEM, se puede lograr esto, por ejemplo, evaluando nudos definidos geométricamente o utilizando puntos de resultados de superficie adicionales.

Las simulaciones realizadas mediante el método de los elementos finitos se basan en lo que se conoce como discretización. En este caso, se descompone un problema con una solución desconocida Se puede controlar el mallado en RFEM utilizando varios ajustes de malla. Puede ser aconsejable no refinar el modelo entero si los resultados dependen de la malla local. Para este propósito, RFEM proporciona la opción de refinamiento local de la malla de EF.

• Manual en línea de RFEM 6 | Cálculo | Malla de elementos finitos

Ejemplo de flexión en voladizo

Como ya se ha mencionado, la forma más fácil de lograr la convergencia es observando las deformaciones. A continuación, se puede ver un ejemplo según Bernd Klein [1] que examina la influencia del mallado en el desplazamiento final de un voladizo. El modelo consiste en un voladizo de aluminio con una longitud de 100 mm y un módulo de elasticidad de 70 GPa. La sección transversal es una placa plana vertical con una altura de 20 mm y una anchura de 1 mm. Se aplica una carga de 1 kN en el extremo del voladizo.

[1] Klein, B. (1997). Basis and applications of the finite element method. Braunschweig/Wiesbaden: Vieweg Verlag.

Estudio de convergencia de malla | Viga en voladizo

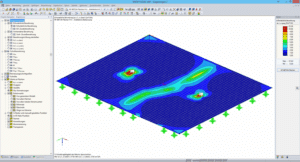
El objetivo es estudiar la deformación en el extremo del voladizo, que se modeló mediante superficies, en función de la densidad de malla. Además, se analizaron diferentes tipos de mallado, elementos triangulares y cuadriláteros. A modo de comparación, el modelado también se realizó utilizando elementos de viga, con (Timoshenko) y sin (Bernoulli), considerando la deformación cortante. El modelo de elementos viga y cuadrilátero, así como los resultados obtenidos, se muestran en la siguiente imagen.

Estudio de convergencia de malla | Deformación de voladizo con distintos enfoques

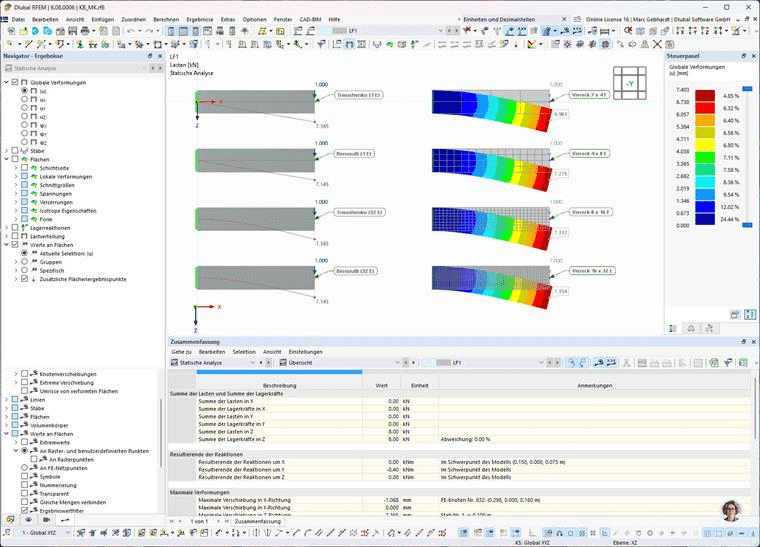
Como puede verse, el mallado del elemento viga no influye en este caso en la deformación del nudo extremo. Sin embargo, la deformación por cizalladura sí se tiene en cuenta, como era de esperar. La deformación sin distorsión de cizalladura (Bernoulli) es menor, de 7,145 mm, que según Timoshenko, de 7,365 mm. Las deformaciones de las superficies en voladizo se aproximan a este valor a medida que aumenta el refinamiento del mallado. Estas relaciones son claramente visibles en el diagrama siguiente.

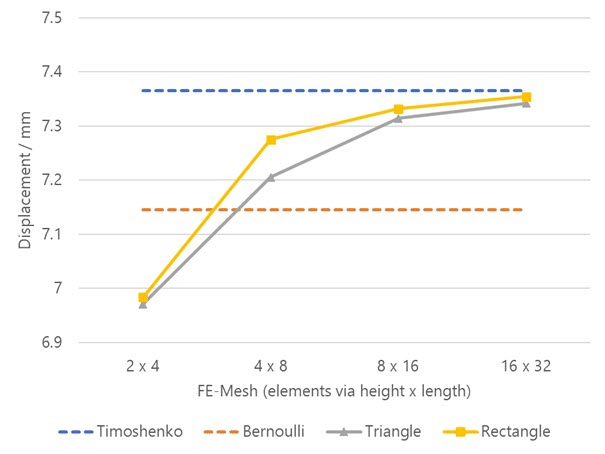
Estudio de convergencia de malla | Diagrama de deformación de ménsula con diferentes enfoques

Ejemplo de tensión y deformación en una placa

El siguiente ejemplo muestra la influencia del mallado en los resultados calculados de tensiones y deformaciones. Para ello, se modeló una superficie con una carga rectangular libre y apoyos de líneas de elevación.

Estudio de convergencia de malla | Superficie

La convergencia del mallado se comprueba en un punto de resultado de superficie situado en una esquina de la carga rectangular libre. La siguiente imagen ilustra este principio. La ventana superior muestra el modelo con mallado, la del medio las primeras tensiones principales obtenidas y la inferior las de las primeras deformaciones principales. El mallado aumenta en los modelos de izquierda a derecha.

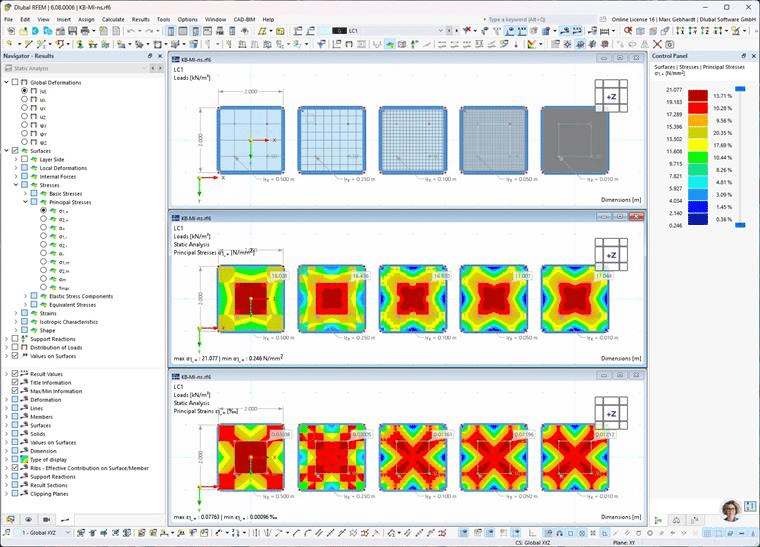
Tensión y deformación en el estudio de convergencia de mallas.

El siguiente diagrama muestra la aproximación de los valores de tensión y deformación con el aumento de la finura de malla hasta un valor límite, conocido como comportamiento de convergencia. Como no es fácil determinar aquí el valor real de la tensión, es aconsejable evaluar el cambio relativo en comparación con el paso de mallado anterior. Esto se muestra en la parte inferior del diagrama. Con una longitud de elemento FE objetivo de 0.01 m, tanto la tensión como la deformación se desvían sólo un 0.2% del paso de refinamiento anterior.

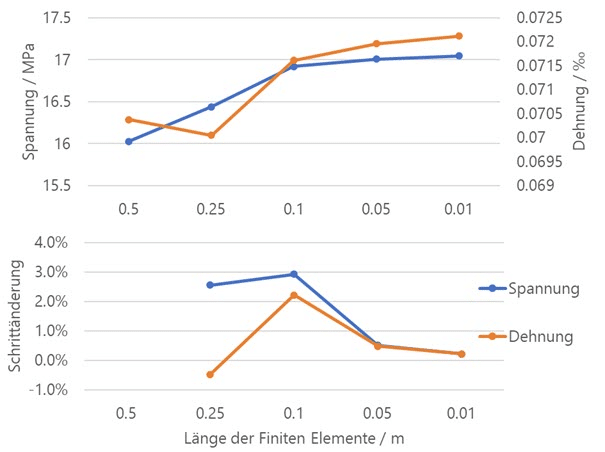
Mesh Convergence Study – Stress and Strain Diagram

Notas finales

Los ejemplos aquí seleccionados pretenden mostrar un procedimiento simplificado para el estudio de la convergencia de la malla. No obstante, hay que tener en cuenta que otros parámetros pueden ser objeto de esta investigación en simulaciones individuales. Además, distintos factores pueden dar lugar a requisitos diferentes. Éstos pueden ser de naturaleza geométrica, por ejemplo, cuando una curvatura debe ser representada con gran precisión por los elementos. Asimismo, el análisis de los daños locales (por ejemplo, el comportamiento de rotura frágil) requiere una malla comparativamente más fina que para la plastificación. Si no se produce una aproximación a un valor límite al aumentar el refinamiento de la malla, podría tratarse de un problema de singularidad. Encontrará más información al respecto en el artículo técnico del siguiente enlace.

• KB | Singularidades en el diseño de superficies de hormigón armado