📚📙 De interés…

Artículo técnico

En la publicación anterior, Pandeo lateral en estructuras de madera | Los ejemplos 1 ilustran la aplicación práctica para determinar el momento crítico de flexión M_crit o la tensión crítica de flexión σ_crit para la inclinación de una viga a flexión por medio de ejemplos simples. En este artículo, el momento flector crítico se determina teniendo en cuenta un apoyo elástico resultante de un arriostramiento.

Modelo estático

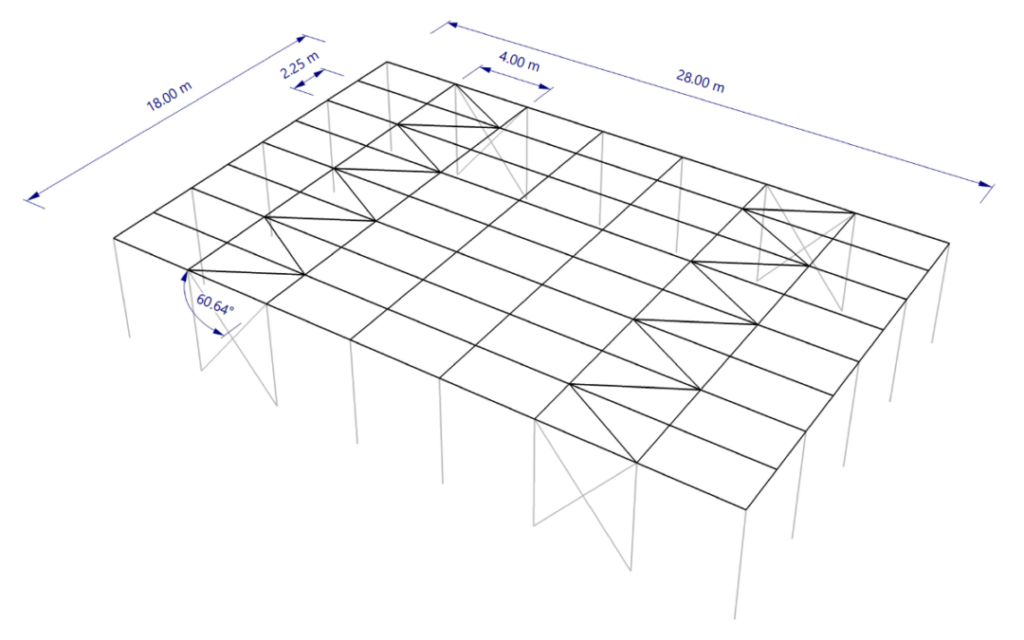
Para el sistema que se muestra en la figura 01, las cerchas se deben analizar para determinar la inclinación. En el nivel de la cubierta, hay seis cerchas como vigas paralelas con una longitud de 18 m y dos arriostramientos de refuerzo. Las vigas en los lados del hastial están apoyadas por pilares y no se consideran para el cálculo. Una carga de cálculo q_d de 10 kN/m actúa sobre las cerchas.

Datos del modelo

Tenga en cuenta: Incluso si las siguientes ecuaciones para E y G no se refieren explícitamente a los valores del cuantil del 5% en el índice, se han tenido en cuenta en consecuencia.

Viga de un vano con apoyos bifurcados sin apoyos intermedios

En aras de la integridad, primero se analiza la cercha sin apoyo lateral (ver figura 02). La longitud equivalente de la barra resulta de una aplicación de carga en el lado superior de la cercha con a₁ = 1,13 y a₂ = 1,44 como sigue:

• Longitud de la barra equivalentel_ef = 17,79 mEl momento crítico de flexión se puede calcular de la siguiente manera:
• Momento flector crítico

M_crit = 134,52 kNm

En estos ejemplos no se muestra un aumento del producto de los cuantiles del 5%de los parámetros de rigidez debido a la homogeneización de las vigas hechas de madera laminada encolada.

El momento flector que actúa sobre las cerchas da como resultado:

• Momento factorizado

M_d = 405,00 kNm

El análisis de valores propios con el módulo adicional RF-/FE-LTB proporciona un factor de carga crítica de 0,3334. El momento crítico de flexión se deriva de esto

M_crit = 0,3334 405 kNm = 135,03 kNm

y por lo tanto es idéntico al resultado de la solución analítica.

Como era de esperar para esta cercha esbelta sin apoyo, el momento flector actuante es mayor (en un factor de 3) que el momento flector crítico y, por lo tanto, la cercha no está suficientemente sujeta contra la inclinación. Sin embargo, un arriostramiento debería contrarrestar esto, que ahora se considera para el cálculo.

Viga de un solo vano con coacción lateral y torsional con apoyos intermedios rígidos

Si el arriostramiento es lo suficientemente rígido, la distancia de los apoyos laterales (por ejemplo, por correas) se usa a menudo como una longitud de barra equivalente para el cálculo inclinado. Por lo tanto, se usa 2.25 m como L. Para un₁ = 1,00 y un₂ = 0,00, sigue:

• Longitud de la barra equivalente

l_ef = 2,25 m

Para el momento flector crítico, se obtienen los siguientes resultados:

• Momento flector crítico

M_crit = 1.063,51 kNm

Dado que el momento flector que actúa sobre la viga es menor que el momento flector crítico, la viga no corre peligro de pandeo lateral bajo la suposición de apoyos intermedios rígidos.

El análisis de valores propios con el módulo adicional RF-/FE-LTB proporciona un factor de carga de pandeo crítico de 2,7815 como resultado. Esto resulta en el momento crítico de flexión

• Momento flector crítico

M_crit = 2,7815 ⋅ 405 kNm = 1,126.50 kNm

Viga de un solo vano con coacción lateral y torsional y apoyo elástico en la barra

La determinación de la longitud de barra equivalente con el factor α y β. Por lo tanto, es posible considerar la rigidez a cortante de un arriostramiento de refuerzo para la inclinación de las cerchas. La rigidez a cortante del arriostramiento se puede determinar según la figura [2] 6.34, por ejemplo. Como se puede ver en esto, esto depende del tipo de arriostramiento, la rigidez a tracción de las diagonales y los postes, la inclinación de las diagonales y la flexibilidad de los medios de fijación. Para el arriostramiento mostrado en la figura 01, la rigidez a cortante da como resultado:

• Rigidez a cortante ideal del arriostramiento

Aquí, E_{D es} el módulo de elasticidad de las diagonales y A_{D es} su área de la sección transversal. Sin embargo, la ecuación anterior no incluye la flexibilidad de los elementos de fijación de las diagonales. Esto y el alargamiento de la barra de las diagonales se pueden considerar por medio de un área de sección ficticia A_D ‘. Por lo tanto:

• Rigidez a cortante ideal del arriostramiento

Donde

• Área de la sección transversal teórica de las diagonales

Las diagonales tienen la dimensión w/h = 120/200 mm y una longitud L_D de 4,59 m. El módulo de desplazamiento de la conexión en cada lado de las diagonales debe ser de 110 000 N/mm.

El área ideal es en consecuencia

A_D ‘= 12,548 mm²

y por lo tanto la rigidez a cortante de un arriostramiento con un ángulo de las diagonales a la cuerda de 60,64 °,

• Rigidez a cortante ideal del arriostramiento

s_id = 44.864 kN

La cimentación de la barra por arriostramiento se puede convertir según la fórmula [2] 7.291 de la siguiente manera:

• Cimentación de barra elástica por arriostramiento

Para dos arriostramientos y seis cerchas, está disponible la siguiente constante elástica por cercha:

• Cimentación de barra elástica por celosía

K_y = 455,6 kN/m² = 0,456 N/mm²

Siempre que K_G = ∞, K_θ = 0, K_y = 0,456 N/mm², e = 600 mm, a₁ = 1,13 y a₂ = 1,44, la longitud de barra equivalente da como resultado:

• Longitud de la barra equivalente

lef = 0,13

El momento crítico de flexión da como resultado un valor utópico de:

• Momento flector crítico

M_crit = 18.482,84 kNm

Se esperaría un valor similar al del sistema con apoyos intermedios rígidos. Como se describe en Pandeo lateral en la construcción de madera: teoría , la aplicación de la fórmula ampliada con α y β tiene una aplicación limitada. Estrictamente hablando, solo es válido si hay una deformación en un arco sinusoidal grande. En otras palabras, si la base es muy blanda. Esto ya no se da en este ejemplo. Las funciones propias de ondas múltiples, que conducen a una pequeña carga de pandeo crítica para cualquier constante elástica más grande, no se incluyen en la ecuación mencionada anteriormente, ya que se basa en aproximaciones del seno monomio.

Como puede ver en la Imagen 07, un vector propio de ondas múltiples resulta del análisis de valores propios.

En este caso, se puede aplicar el método derivado del Prof.Dr. Heinrich Kreuzinger (2020). El momento crítico de flexión se calcula como sigue:

La constante n denota la 1ª, 2ª, 3ª … resolución propia. Por lo tanto, se deben analizar varias soluciones propias y entonces determina el momento flector crítico más pequeño. Los siguientes momentos críticos de flexión son el resultado para n = 1… 30.

M_{crit se} vuelve mínimo para n = 6 y es de aproximadamente 1.282,70 kNm.

La solución de valores propios del módulo adicional RF-/FE-LTB (ver imagen 07) da como resultado:

M_crit = 3.4376 ⋅ 405 kNm = 1.397.25 kNm

Ambos resultados coinciden muy bien. Sin embargo, la solución analítica es segura, ya que este método se basa en una distribución constante del momento flector. Luego, se asigna una carga crítica q_crit al momento flector crítico constante M_crit .

• Carga crítica

Dado que la cimentación de la barra en este ejemplo se considera muy rígida y se distribuye constantemente sobre la longitud de la barra de la cercha, se producen momentos flectores críticos que son ligeramente más altos que para los apoyos individuales rígidos.

Según [3] Capítulo 9.2.5.3 (2), los arriostramientos de rigidización deben ser lo suficientemente rígidos como para no exceder la flecha horizontal de L/500. El cálculo se debe realizar con los valores de cálculo de las rigideces (ver [1] Capítulo NCI hasta 9.2.5.3).

Para k_crit = 0,195, H = 5 m y q_p = 0,65 kN/m² como presión de velocidad de ráfaga, se obtienen las siguientes cargas (véase [3], capítulo 9.2.5.3):

• Fuerza estabilizadora para el ala comprimida

N_d = (1 – 0,195) ⋅ 405/1,2 = 271,68 kN

• Carga de rigidez

q_d = 2,76 kN/m

• Carga de cálculo del viento

q_{d, viento} = 1,5 ⋅ (0,7 + 0,3) ⋅ 0,65 ⋅ 5/2 = 2,44 kN/m

La deformación del arriostramiento de rigidización se muestra en la Imagen 08. Las cargas se dividieron por la mitad porque hay dos arriostramientos de refuerzo.

La deformación admisible es:

• Deformación admisible

El resultado confirma la suposición de un arriostramiento muy rígido y es consistente con los momentos críticos de flexión casi idénticos del sistema con apoyos intermedios rígidos y uno con apoyo elástico de la barra.

Conclusión

Se mostró qué posibilidades en la construcción de madera se pueden utilizar para analizar el pandeo lateral de vigas a flexión. Para los métodos comunes, es importante asegurarse de que los arriostramientos de refuerzo sean lo suficientemente rígidos para aceptar apoyos rígidos. En este artículo se muestran las opciones para el caso de que no se aplique este supuesto. Básicamente, las vigas a flexión y los arriostramientos de rigidización deben diseñarse para su capacidad de carga y servicio según la norma correspondiente. Sin embargo, esto está más allá del alcance de este artículo.

Referencia

[1]	National Annex – Eurocode 5: Design of timber structures – Part 1-1: General – Common rules and rules for buildings; DIN EN 1995-1-1/NA:2013-08
[2]	Petersen, C.: Statik und Stabilität der Baukonstruktionen, 2. Auflage. Wiesbaden: Vieweg, 1982
[3]	Eurocódigo 5: Proyecto de estructuras de madera. Parte 1-1: Reglas generales y reglas para edificación; versión alemana EN 1995-1-1:2004 + AC:2006 + A1:2008. Beuth Verlag GmbH, Berlin, 2008.